Control Volume Switchboard

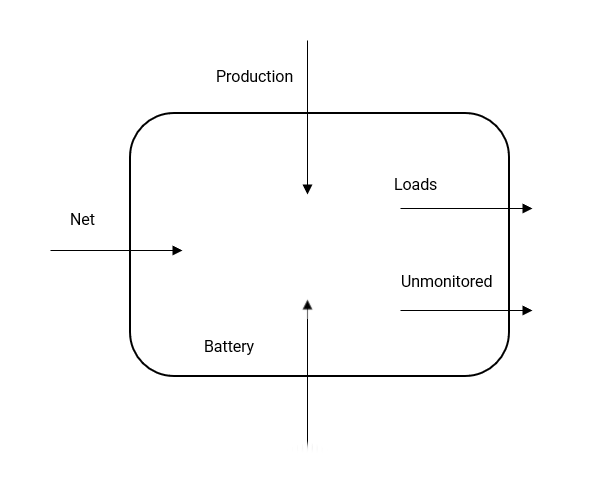
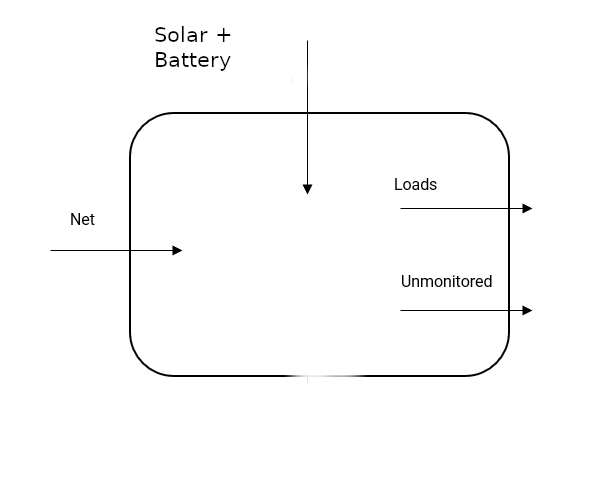
This is how I use a control-volume approach to practically monitor circuits. It’s half maths and half “it’s easy that way”. The area below is a switchboard, monitored with multiple CTs. See phisaver.com.

Referring to the above:

• Net
  • Import is positive, export is negative
• Production is positive
• Loads are positive and monitored
• Unmonitored loads are same as Loads, just without a CT
• Battery is a positive when providing energy (i.e. like Net and Production) and negative when charging. (We are assuming Production === Solar. See alternative: P=B+S, further down)
• Battery is a special case of Load. Positive when changing, negative when discharging. It is not considered in the following.

We can then work out some useful equations. I use them in iotawatts.

• N + P – L – U + B = 0
• U = N + P – L + B

If U=0 (i.e. we monitor all loads):

• B = – N – P + L

Current Transformers

When you plug in your CT to your PCB (e.g. IotaWatt), it has a direction. But which way is which? This is arbitrary. It’s only important for sensors that can go negative (Net, Battery/Production).

In the diagram above have the positive direction point to the switchboard. We ignore loads in this scenario and just make them all positive.

Accu-CT (Canada) – arrow points in negative direction. We reverse the arrow (i.e. draw over it).

Derived Measurements

We can further derive some measurements with cannot be directly sensed. There can be found on the Iotawtt:

• Import : Net max 0
• Export: (Net max 0) x -1
• Unmonitored: Net + Production – (monitored) Loads
• Consumption: Net + Production (since Consumption = U+L and U+L = N+P)

Some further notes on these measures.

• Production and consumption are not at the meter, as production can be self-consumed.
• Production is of any kind (e.g. solar, battery, whatever). Battery storage within the building is consider production, it’s just shifted in time.
• Net is “at the meter”.
• It’s help to record Import and Export, because we can easily sum them. You can’t sum Net, then get Export: you have to get Export at each time then sum. This is because the positives and negatives of Net can cancel.

Given that:

Net = Import - Export 

Net = Consumption - Production

.. then putting this together:

Production - Export + Import - Consumption = 0

Import Consumption v Free Consumption

We want to state (e.g.) “your solar system covers x % of your energy”. This is a bit tricky. Imagine over two days:

• Day 1: 10 kWh consumption, no production (broken)
• Day 2: 10 kWh consumption, 20kWh production (exactly balanced)

So, do we mean:

• Option A: Fraction of consumption directly (i.e. behind the meter) provided by solar. If so, then that’s 10kWh / 20 kWh or 50%. This is, perhaps, a more accurate measure of solar contribution.
• Option B: Fraction of consumption provided by solar (either directly, or exported-then-imported). If so, then that’s 20kWh / 20kWh or 100%. The general definition of “Net Zero” is 100%.

Let’s break consumption up…

 Consumption = Consumptionfree (i.e. behind meter, from onsite production ) +    Consumptionimported (i.e. imported from Grid) 

… and then work out ImportConsumption and FreeFraction for the two options

Option A: “Direct”

ImportFractiondirect  = Import / Consumption
FreeFractiondirect = 1 - ImportFractiondirect 
            
...and by the way...
FreeFractiondirect = Consumptionfree / Consumption 
FreeFractiondirect =  (Production - Export)  / Consumption 

Option 2: “Net”

FreeFractionnet = Production / Consumption
FreeFractionnet = 1 - FreeFraction

Self-Produced Consumption versus Grid Consumption

Recall we split total consumption, C, into “Consumption from onsite production (free)” and “Consumption from imported grid energy(imported)”, or:

(1) C = Cfree + Cimported 

We also know that C_free, or “from onsite production” is the onsite Production, less anything Exported:

(2) Cfree = P - E

and so we can re-arrange and substitute to find:

Cimported = C - Cfree
Cimported = C - P + E

This is useful for PhiSaver as we monitor Production and Export directly, so can calculate C_free “free energy / onsite consumption / wadeveryoucalit ” and compare to C_imported

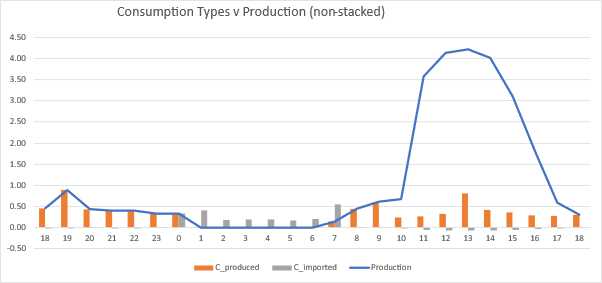
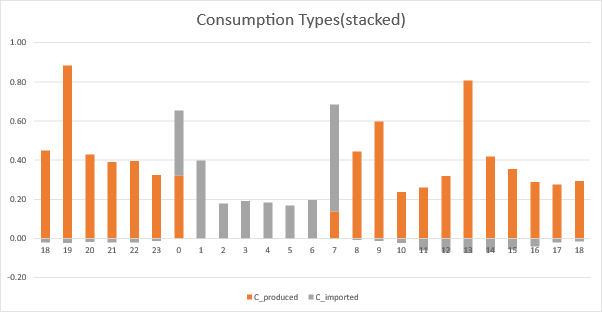
We see some sample data below. When solar is active, it’s all C_free (solar used on site). At night when production (integrated battery) expires at midnight, we import. The second chart just shows for a given hour (e.g. 00:00 to 01:00 and 07:00 to 08:00) we have both “produced” and “imported” consumption.

Consumption, Unmonitored and ConsumptionNet

Imagine we’ve got a big switchboard with 40 poles. It’s impractical to monitor each circuit – we tong/guess to monitor the big users. Let’s say we cover 20 poles, with 90% of the load. Great! But what about the 10%? How do we report that?

ConsumptionNet is the real consumption. It’s Net + Production at the board. It’s 100% of the load.

ConsumptionMonitored is the sum of monitored circuits. It’s 90% of the load in our case.

Unmonitored is the difference (10% in our case)

Ideally we’d report this from an iotawatt, but the calculation is difficult and error prone. Instead we calculate it:

Consumption(Net) = Net + Production

Umonitiored = ConsumptionNet - ConsumptionMonitored

For convenience we do this:

1. Iotawatt and Iotawatt bucket: Iotawatt Consumption is ConsumptionMonitored
2. Influx (power, energy) buckets: Consumption calculated (as ConsumptionNet). ConsumptionMonitored is removed and Unmonitored takes it’s place.

One question: we can calculate ConsumptionNet in two ways; are they equilivant:

1. ConsumptionNet = Sum (Net) + Sum(Production) : sum first, then add
2. ConsumptionNet = Sum(Net + Production): sum each interval, then add results

And yes, I did a numerical test and it seems these are equivalent. I thought the -ve of Net would stuff up #1. But the maths…. dunno: F(x) + F(y) = F(x+y)?

Proportions of Averages versus Averages of Proportions

TLDR> When doing proportions (solar fraction, etc) take the fraction of the averages. That is, first take the sum or mean, then divide. An example is below.

Time	Consumption	Import	ImportConsumptionFraction
time1	0.05	0.00	0.00
time2	1.76	1.50	0.85
time3	1.66	1.65	0.99
time4	1.82	1.82	1.00
Average of columns:	1.32	1.24
		0.94	0.71
		Fraction of Average	Average of Fractions
		CORRECT	INCORRECT

Import, Export, Net

For single phase:

Export = Net [-oo,0] * -1

Import = Net [0,+oo] *

No worries, but for three phase there are two options for import/export

1. Export = ((NetR min 0) + (NetW min 0) + (NetB min 0)) x -1
2. Export = ((NetR + NetW + NetB) min 0)) x -1

And also, Net = NetR + NetW + NetB and Import is similar to Export, just with the x -1

What? Well with #1 we treat each phase separately. Maybe Red is exporting and White is importing. For #2 we sum them together. Imagine #1 is 3 pipes measured separately, and #2 is putting the 3 pipes into 1 pipe then measuring that.

For example at a moment in time:

• Red: -10 Blue: 5 White: 20

1. Net is 15. Export is -10 and import is 25. This is really happening: simultaneous import and export is real.
2. Net is 15. Export is 0 and Import is 15. This is a simplification.

I don’t know how utility meters handle this. #1 or #2 or something different?

Batteries (in progress)

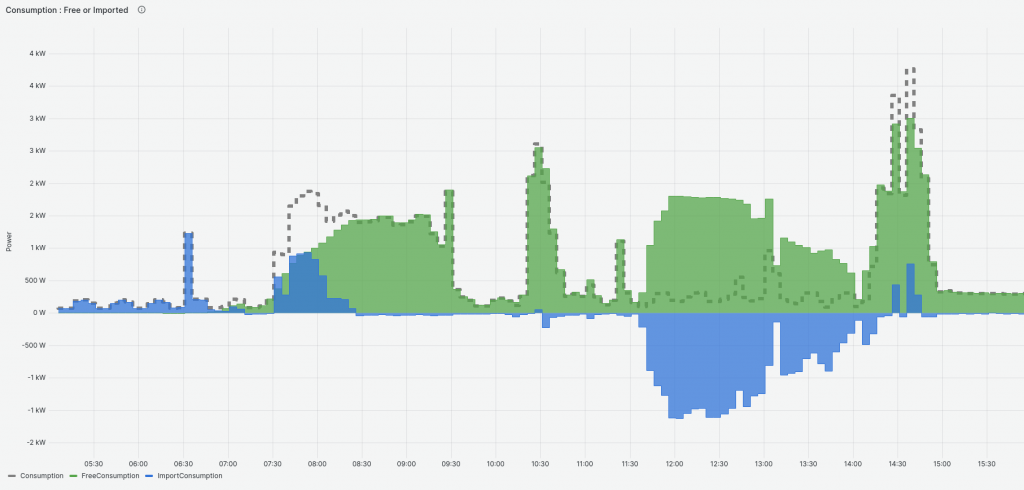
The equations above assume no battery. But look what happens when I try it on some sites without and with a battery:

Without a battery, below: the green (“free”) and blue (“imported”) add to the dashed (total) Consumption. All good.

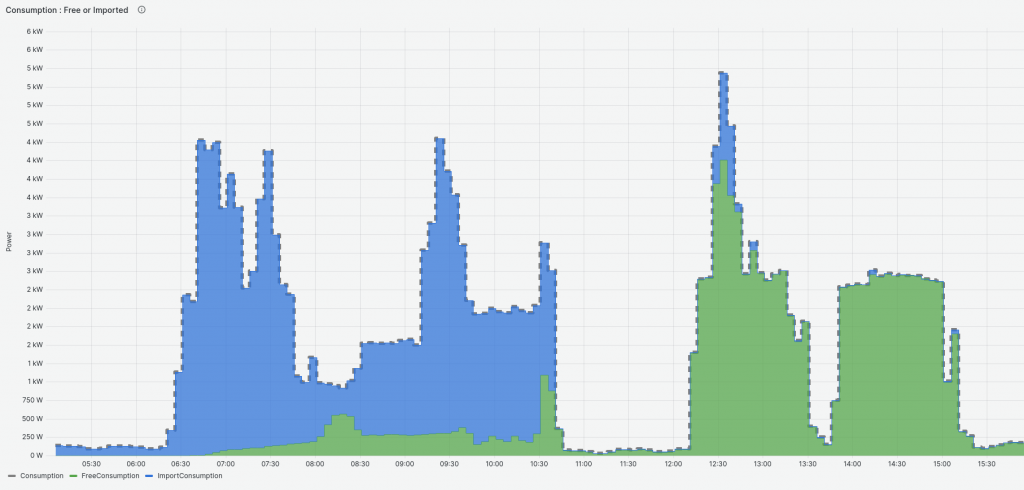
With a battery, below, “free” and “imported” don’t add to “total”. We need to add in a battery storage element. On the left at 08:00, consumption (dashed) is higher than free+import. The different must be changing to battery. On the right (12:30), consumption is lower than “free” and “import” is negative! This ain’t exporting (we accounted for that), it’s changing the battery.

Initially, I thought we could deduce battery charge/discharge:

B = -N + P + L

But, in this site’s case (and it’s common), the Production is actually Battery+Solar. That is, the battery doesn’t directly feed into our switchboard (as in our original control volume). We actually have:

Given that P = B + S, we cannot differentiate between B and S. We don’t have any equations between them. We actually have:

N + P – L – U = 0

N + B + S – L = 0 # assume U=0 and use P=B+S

Bummer. Can we be clever? Maybe a little. We know solar works in the day, so S=0 at night. Also, L>0. So we could approximate B/P breakdown. This is the intuitive thinking from the graph above.

This is might work if Battery is directly connected to switchboard

So let’s whack in a Battery (B) term. Let definite +ve as discharging (like ‘importing’ is +ve for Net) and -ve as charging (like ‘exporting’ is -ve for Net). It’s perhaps kinda like another Export term. We already know

(1) B = - N - P + L

(1) B = - N - P + C

ps. Loads = Consumption.

We also know Ctotal (direct sum of all loads)

(2) C = Cfree + Cimported

We also how that C_produced, or “from onsite production” is the onsite Production, less anything Exported, and less anything to Battery.

(?) Cfree = P - E - B ???

and so we can re-arrange and substitute to find:

Cimported = C - Cfree - B ???
         = C - (P-E-B) - B
         = C - P + E 

Arrggghhh, don’t know. I think we have knowns: C, P, E and unknown Cfree,Cimported and B and only two equations. But going back to (1), less take B=0 to start. If C > C_free+Max(0,C_import) then B_charge = C-C_import and if C<C_free+Max(M,C_import) then B_discharge = Cfree-abs(Cimport)

Yeah, I think we can use the knowledge that C_free and C_import must be both (a) positive and (b) less then C to “make up” for the missing equation (i.e. 3 unknowns, 2 equations).

Need maths help!